Angle transformation to [-π, π]
One thing that can be hard to get right is the mapping from -∞ to ∞ radians to -π to π radians. Or -∞ to ∞ to -180° to 180°. I’ve been unable to find information about it with Google (except for the functions that comes with Matlab), so I decided to share a function I’ve made that does the transformation.
In C#:
void TransformToPipi(double inputAngle, out double outputAngle, out int revolutions)
{
revolutions = (int)((inputAngle + Math.Sign(inputAngle) * Math.PI) / (2 * Math.PI));
outputAngle =
(inputAngle + Math.Sign(inputAngle) * Math.PI) % (2 * Math.PI) -
(Math.Sign(Math.Sign(inputAngle) +
2 * (Math.Sign(Math.Abs(((inputAngle + Math.PI) % (2 * Math.PI))
/ (2 * Math.PI))) - 1))) * Math.PI;
}
The function takes an angle in radians as input and outputs an angle between -π and π, as well as the number of revolutions it takes to get there. The output angle is in radians too of course.
Here is an example:
double inputAngle = 3.5 * Math.PI;
double outputAngle;
int revolutions;
TransformToPipi(inputAngle, out outputAngle, out revolutions);
Console.WriteLine(
"input angle = {0:f}, output angle = {1:f}, revolutions = {2}",
inputAngle, outputAngle, revolutions);
// input angle = 11.00, output angle = -1.57, revolutions = 2
The same function can be written like this in Python:
import numpy as np
from math import fabs, pi
def transform_to_pipi(input_angle):
revolutions = int((input_angle + np.sign(input_angle) * pi) / (2 * pi))
p1 = truncated_remainder(input_angle + np.sign(input_angle) * pi, 2 * pi)
p2 = (np.sign(np.sign(input_angle)
+ 2 * (np.sign(fabs((truncated_remainder(input_angle + pi, 2 * pi))
/ (2 * pi))) - 1))) * pi
output_angle = p1 - p2
return output_angle, revolutions
The difference here is the use of truncated_remainder() rather than %.
There are three types of remainder calculations according to Wikipedia:
- using truncated division
- using floored division
- using Euclidean division
Python uses floored division when finding the remainder with %. In short, that means -5 % 2 = 1, not -1. The algorithm above has to use truncated division when calculating the remainder, so we have to define our own function that does that:
def truncated_remainder(dividend, divisor):
divided_number = dividend / divisor
divided_number = \
-int(-divided_number) if divided_number < 0 else int(divided_number)
remainder = dividend - divisor * divided_number
return remainder
If we plot the input of transform_to_pipi() vs. the output we get:
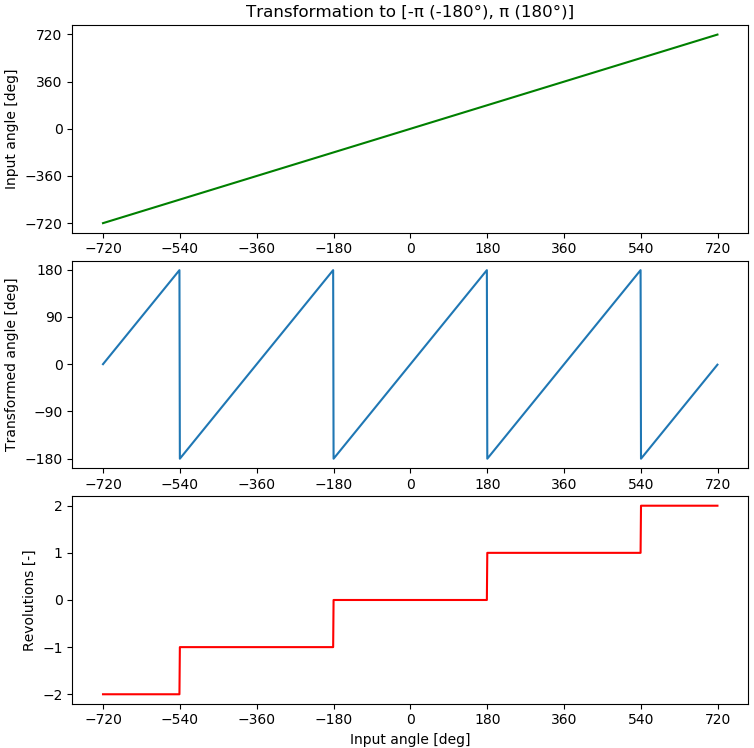
The transformed angle stays within -π (-180°) and π (180°) when the input angle increases. The revolution counter is incremented when the output angle reaches π (180°).
The script for plotting the transformation looks like this in case anyone is interested:
import matplotlib.pyplot as plt
import numpy as np
from math import fabs, pi, radians
start = -720.0
stop = 720.0
step = 1.0
angles_deg = np.arange(start, stop, step)
angles_rad = np.arange(radians(start), radians(stop), radians(step))
transformed_angles = []
transformed_revolutions = []
for angle in angles_rad:
transformed_angle, transformed_revolution = transform_to_pipi(angle)
transformed_angles.append(transformed_angle * 180.0 / pi)
transformed_revolutions.append(transformed_revolution)
plt.subplot(3, 1, 1)
plt.xticks(np.arange(min(angles_deg), max(angles_deg) + 10, 180.0))
plt.title("Transformation to [-π (-180°), π (180°)]")
plt.yticks(np.arange(min(angles_deg), max(angles_deg) + 10, 360.0))
plt.plot(angles_deg, angles_deg, 'g')
plt.xlabel("Input angle [deg]")
plt.ylabel("Angle [deg]")
plt.subplot(3, 1, 2)
plt.xticks(np.arange(min(angles_deg), max(angles_deg) + 10, 180.0))
plt.plot(angles_deg, transformed_angles)
plt.yticks(np.arange(min(transformed_angles), max(transformed_angles) + 10, 90.0))
plt.xlabel("Input angle [deg]")
plt.ylabel("Transformed angle [deg]")
plt.subplot(3, 1, 3)
plt.xticks(np.arange(min(angles_deg), max(angles_deg) + 10, 180.0))
plt.yticks(np.arange(-2, 2 + 0.1, 1))
plt.plot(angles_deg, transformed_revolutions, 'r')
plt.xlabel("Input angle [deg]")
plt.ylabel("Revolutions [-]")
plt.show()
Going from -π,π angle and revolutions to -∞,∞ angle is as easy as
infinf_angle = pipi_angle + revolutions * 2.0 * pi