Trajectory generators are necessary in control systems when we want to move something smoothly from some initial position to another position. They are often very advanced and derived from first principles for a particular system. So I was searching the Internet for something that was fast and easy to implement and luckily enough I found the minimum jerk trajectory.

The minimum jerk trajectory is based on minimizing the sum of the squared jerk (time derivative of acceleration) along its trajectory. I won’t go into details on how it’s derived, but just show the final equation in the paper:

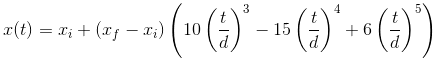
Position equation

x_i is the current position, x_f is the setpoint, t is travel time, d is how long it should take to get from the current position to the setpoint. The units of x_i and x_f are, for example, meters, degrees or radians. The dimension is distance. The unit of t and d is typically seconds. The dimension is time.

The velocity trajectory is also nice to have. You can’t find it in the paper, but it’s easy to find on our own by finding the time derivative of the position equation:

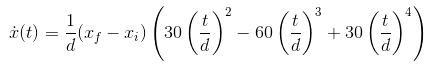
Velocity equation

As you can see there is very few tuning parameters for the trajectory. The only thing that can be changed is d: the time it should take to get to the final position. The upside is that we have two explicit equations that are very easy to implement that will give a decent result.

Code

The equations can be translated into the code shown below. I chose to use Python here because it’s borderline pseudo code and allows me to use matplotlib for plotting.

mjtg accepts the current position (start position), the setpoint (desired position), the frequency of the control system and a time parameter that indicates how long it should take to get from the current position to the setpoint.

We can also use average velocity rather than movement time, considering that we know the position delta and time (v = p/t after all). Average velocity is used in the example below.

We must take frequency into account, otherwise the trajectory will run too fast (higher than 1 Hz) or too slow (lower than 1 Hz). It’s not important in the sample below, but it has to be taken into account for real systems. d in the equations is replaced with timefreq = d * f.

import matplotlib.pyplot as plt
import numpy as np


def mjtg(current, setpoint, frequency, move_time):
    trajectory = []
    trajectory_derivative = []
    timefreq = int(move_time * frequency)

    for time in range(1, timefreq):
        trajectory.append(
            current + (setpoint - current) *
            (10.0 * (time/timefreq)**3
             - 15.0 * (time/timefreq)**4
             + 6.0 * (time/timefreq)**5))

        trajectory_derivative.append(
            frequency * (1.0/timefreq) * (setpoint - current) *
            (30.0 * (time/timefreq)**2.0
             - 60.0 * (time/timefreq)**3.0
             + 30.0 * (time/timefreq)**4.0))

    return trajectory, trajectory_derivative

# Set up and calculate trajectory.
average_velocity = 20.0
current = 0.0
setpoint = 180.0
frequency = 1000
time = (setpoint - current) / average_velocity

traj, traj_vel = mjtg(current, setpoint, frequency, time)

# Create plot.
xaxis = [i / frequency for i in range(1, int(time * frequency))]

plt.plot(xaxis, traj)
plt.plot(xaxis, traj_vel)
plt.title("Minimum jerk trajectory")
plt.xlabel("Time [s]")
plt.ylabel("Angle [deg] and angular velocity [deg/s]")
plt.legend(['pos', 'vel'])
plt.show()

This is the result:

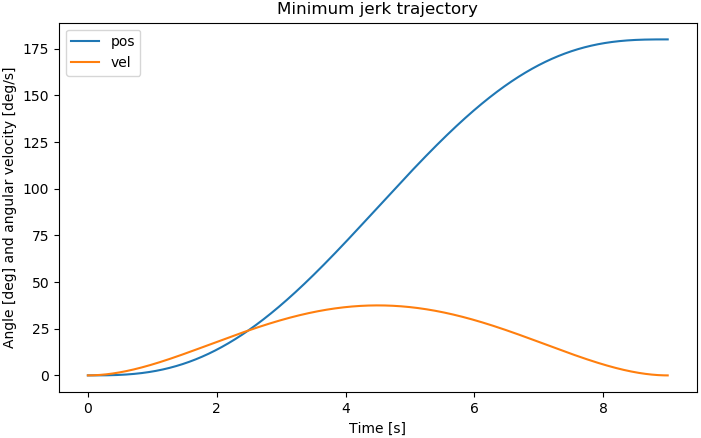
Minimum jerk trajectory 1

The trajectory moves from 0 to 180° in a smooth manner. It takes 180° / 20°/sec = 9 sec as it’s supposed to, because the average velocity is 20°/sec. The maximum velocity seems to be 1.87 times larger than the average velocity, quite consistently. It peaked at about 37.5°/sec for this example.

If the maximum velocity of the process is known, and we want to go as fast as possible, we can choose the average velocity to be the maximum velocity divided by 1.87. E.g. a servo motor can move at maximum 50°/sec. That means the velocity in the code above would be set to 50/1.87 = 26.7°/sec.

average_velocity = 26.7
current = 0.0
setpoint = 180.0
frequency = 1000
time = (setpoint - current) / average_velocity

traj, traj_vel = mjtg(current, setpoint, frequency, time)

# Plot here
# ...

Result:

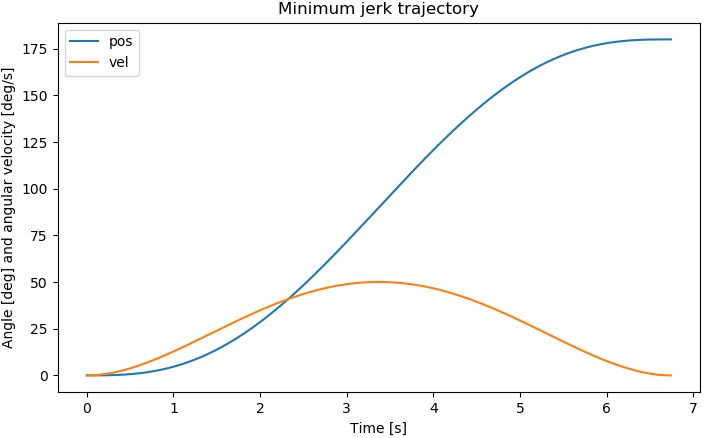
Minimum jerk trajectory 2

And we see that the maximum velocity is 50°/sec like wanted.